노튼의 정리(노턴의 정리)는 복잡한 회로를 간단하게 만드는 또 하나의 정리 방식입니다.
테브난의 정리랑 어떤 방식이 다른지 비교해 보고, 적용하는 법을 알아가 봅시다.
목차
노튼의 정리
노튼의 정리 정의

노튼의 정리란 전류원과 저항으로 회로를 정리하는 방법을 말합니다.
전류원과 병렬 저항 1개로 복잡한 회로를 요약하는 것입니다.
테브난의 정리와 비슷하지만, 전류원이라는 특징이 있습니다.
전원의 성질이 다르기 때문에 구하는 방식도 다릅니다.
등가회로를 만드는 이유는 테브난의 정리와 똑같습니다.
테브난 등가회로의 개념은 이전 포스팅을 참고하시길 바랍니다.
2023.04.18 - [회로이론/처음해보는 회로이론] - 기초 회로 이론 16. 테브난 정리(테브난 등가회로) 및 예제
기초 회로 이론 16. 테브난 정리(테브난 등가회로) 및 예제
테브난 정리는 복잡한 회로를 간단하게 만들어주는 정리입니다. 이번 시간에는 간단한 회로에 테브난 정리 적용 방법을 알아보겠습니다. 목차 1. 테브난 정리의 정의 2. 예제 소개 3. 등가 저항(R)
moomoodevelopment.tistory.com
예제

저항 2개와 전류원 1개로 만들어진 예제 회로입니다.
다음과 같은 회로에 노튼 등가회로를 만들어 보겠습니다.
최대한 간단한 회로로도 긴 설명이 이어질 예정입니다.
Rn 구하는 법

등가저항을 구하는 방법은 테브난의 정리와 같습니다.
전압원은 단락, 전류원은 개방을 해서 Rab를 구하는 것입니다.
1. R1은 개방상태입니다.
전류원과 R1은 직렬연결 상태입니다.
저항을 구할 때 전류원을 개방시키면, 저항이 무한대입니다.
전선이 끊기니 전류가 못넘어간다는 것을 무한대라 말하는 것입니다.
그렇기에 무한대+3=무한대로 계산이 이루어집니다.
2. R2는 단락상태입니다.
R2와 따로 연결이 되어있는 전원이 없습니다.
주변에 아무 소자도 없기 때문에 R2 주변은 단락처리합니다.
저항을 그대로 둔다는 말을 주변이 단락상태라 표현한 것입니다.
즉, R2는 따로 계산이 필요하지 않습니다.
3. Rn은 2Ω입니다.
무한대//Rn = R2가 됩니다.
이것은 식보다 개념으로 이해할 수 있습니다.
R1은 전류원에 의해 무한대의 값이 되었습니다.
전류입장에선 전류원 방향의 길이(R1) 끊겨 지나갈 수 없습니다.
즉, 전류는 R2 방향으로만 지나갈 수 있는 것입니다.
그래서 노튼의 정리 등가저항의 값은 Rn = R2 =2Ω입니다.
In 구하는 법

In을 구할 때에는 단자 ab를 선으로 잇는 것이 우선입니다.
(In의 n은 노튼(norton)의 n입니다.)
선 ab에 흐르는 전류 Iab가 곧 In입니다.
1. R2는 무시합니다.
전선과 저항의 병렬연결은 저항이 0입니다.
계산식으로 병렬연결 계산을 해보면 0//R2 = 0Ω입니다.
전류는 저항이 낮은 쪽으로 흐르려는 성질이 있습니다.
저항이 아예 없는 선 ab와 R2의 갈림길이 있습니다.
전류는 당연히 저항이 없는 선 ab로 모두 흐릅니다.
즉, R2는 무시취급해서 없는 것이나 같은 것입니다.
2. In은 10A입니다.
In은 Iab와 같은 전류값입니다.
R2를 회로에서 지우면 오른쪽의 회로가 됩니다.
이렇게 되면 전류원과 선 ab는 직렬연결입니다.
직렬연결일 때 전류는 어디서나 값이 같습니다.
그래서 전류원의 10A가 곧 In입니다.
정답 및 요약
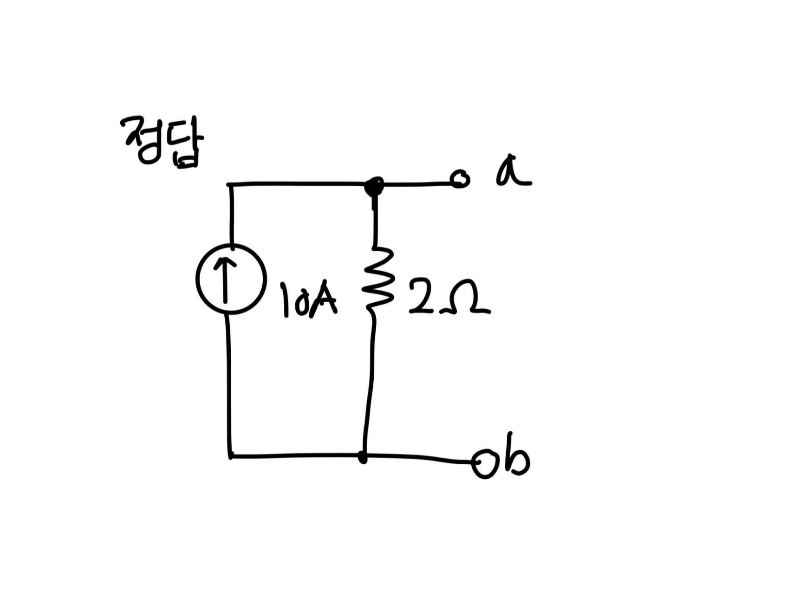
1. 회로의 전원을 단락 혹은 개방한다.
2. Rab(Rn)를 구해준다.
3. ab에 흐르는 전류 Iab(In)를 구한다.
4. 1개의 전류원과 저항으로 정리한다.
위 방식으로 노튼 등가회로를 제작할 수 있습니다.
전류원이 위주인 회로는 노튼 등가회로를 적용합니다.
전압원이 위주로 된 회로는 테브난 등가회로를 사용합니다.
이상 노튼 등가회로 포스팅 마치겠습니다.
'회로이론 > 처음해보는 회로이론' 카테고리의 다른 글
| 기초 회로 이론 19. 중첩의 원리 및 예제(중첩의 정리) (1) | 2023.04.23 |
|---|---|
| 기초 회로 이론 18. 테브난의 정리vs노튼의 정리 비교(전원 변환) (0) | 2023.04.21 |
| 기초 회로 이론 16. 테브난 정리(테브난 등가회로) 및 예제 (3) | 2023.04.18 |
| 기초 회로 이론 15. 폐회로, 개회로(구분방법, 단락 상태, 개방 상태) (0) | 2023.04.15 |
| 기초 회로 이론 14. 델타 와이 변환(Δ-Y,Y-Δ 변환) (2) | 2023.04.11 |




댓글