중첩의 정리는 전원이 여러 개인 모든 회로에 적용이 가능합니다.
회로해석에서 전압, 전류를 구할 때 자주 사용하는 이론입니다.
목차
중첩의 정리
정의

중첩의 정리란 회로를 쪼개서 해석하고 다시 합치는 정리입니다.
회로를 쪼개는 기준은 바로 전원(전압원, 전류원 등)입니다.
전원의 개수만큼 회로를 쪼개서 해석하면 됩니다.
사용하는 경우는 크게 두 가지 있습니다.
- 복잡한 회로를 해석할 때 사용할 수 있습니다.
- 많은 전원을 가지고 있을 때 활용합니다.
예제

예제 회로에서 $I_{T}$의 값을 구해봅시다.
전압원, 전류원 각각 1개가 있는 회로입니다.
즉 회로를 2개로 쪼개서 해석할 예정입니다.
이번 예제에서는 전류값을 구합니다.
$I_{T}=I_{T1}+I_{T2}$
이 식과 같이 전류를 1, 2 번호로 구분하겠습니다.
아래에서 해석 방법을 확인하겠습니다.
전압원 풀이

1. 전류원 개방
전류원을 개방해 회로를 분리합니다.
전류를 일정하게 만드는 것은 저항이 무한대와 같습니다.
이 개념은 전류원 포스팅에서 자세하게 다뤘습니다.
2023.03.22 - [회로이론/처음해보는 회로이론] - 기초 회로 이론 9-2. 전류원의 개념과 전원변환
기초 회로 이론 9-2. 전류원의 개념과 전원변환
오늘은 전류원에 대한 개념과 전압원과의 관계를 알아보겠습니다. 전류원은 회로에서 보는 순간 저도 모르게 얼굴이 찡그려집니다. 저도 이 친구가 그다지 익숙하지 않기 때문입니다. 말썽쟁이
moomoodevelopment.tistory.com
2. 테브난의 정리 적용
답을 구해야 할 부분은 간소화하면 안 됩니다.
파란색 상자 안에 테브난의 정리를 적용했습니다.
이 상자에 제가 구해야 할 전류($I_{T}$)는 포함되지 않습니다.
테브난의 정리가 아니라 다른 방법을 사용해도 됩니다.
회로를 그대로 두고 노드, 메쉬해석법을 사용해도 됩니다.
테브난 등가회로 만드는 법은 이 포스팅에 정리되어 있습니다.
2023.04.18 - [회로이론/처음 해보는 회로이론] - 기초 회로 이론 16. 테브난 정리(테브난 등가회로) 및 예제
기초 회로 이론 16. 테브난 정리(테브난 등가회로) 및 예제
테브난 정리는 복잡한 회로를 간단하게 만들어주는 정리입니다. 이번 시간에는 간단한 회로에 테브난 정리 적용 방법을 알아보겠습니다. 목차 1. 테브난 정리의 정의 2. 예제 소개 3. 등가 저항(R)
moomoodevelopment.tistory.com
3. 옴의 법칙 적용
옴의 법칙으로 회로 1의 전류는 1.5A입니다.
개방된 회로는 연결되지 않은 것과 같습니다.
그래서 2.75Ω과 1.25Ω의 직렬연결로 계산합니다.
6/(2.75+1.25) = 3/2 =1.5
전류원 풀이
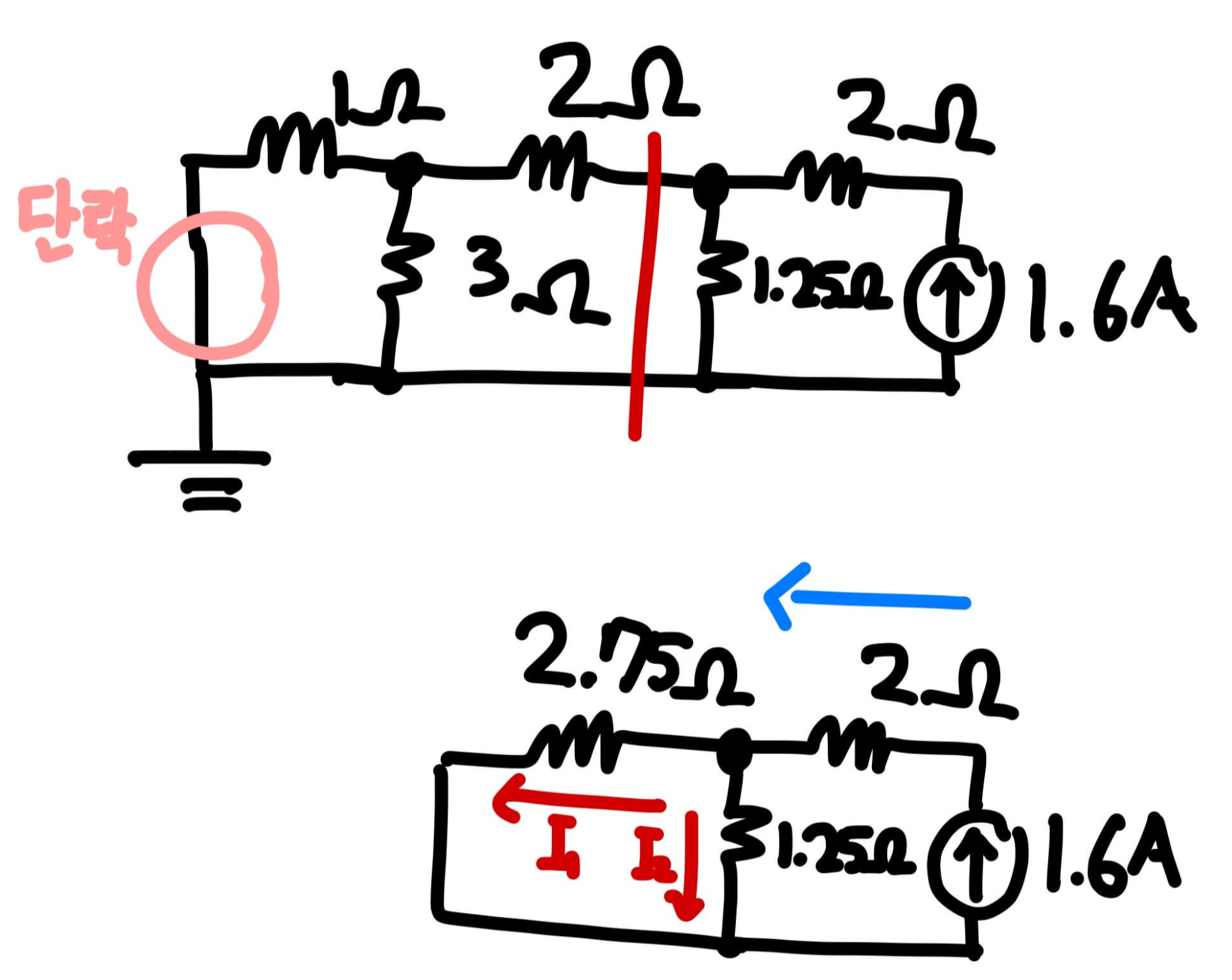
1. 전압원 단락
전압원을 단락해 전류원에 초점을 맞춥니다.
이상적인 전압원은 내부저항이 0입니다.
전류원은 그대로 두고, 전압원을 그림처럼 만듭니다.
2023.03.21 - [회로이론/처음해보는 회로이론] - 기초 회로 이론 9-1. 전압원의 개념과 연결 (feat. 쇼트, 임피던스)
기초 회로 이론 9-1. 전압원의 개념과 연결 (feat. 쇼트, 임피던스)
오늘은 전압원에 대해서 포스팅을 해보려 합니다. 전원의 정의와 특징, 연결할 때 어떻게 해석할지 차례대로 알아보겠습니다. 후에 작성할 전류원, 종속전원과 시리즈로 이어질 예정입니다. 전
moomoodevelopment.tistory.com
2. 테브난의 정리 적용
앞선 회로처럼 간소화 작업을 진행합니다.
간소화 작업은 가지치기를 만드는 효과가 있습니다.
테브난의 정리는 저항만 있어도 적용 가능합니다.
답을 구할 1.25Ω 부분은 변환하지 않습니다.
3. 저항과 전류의 비
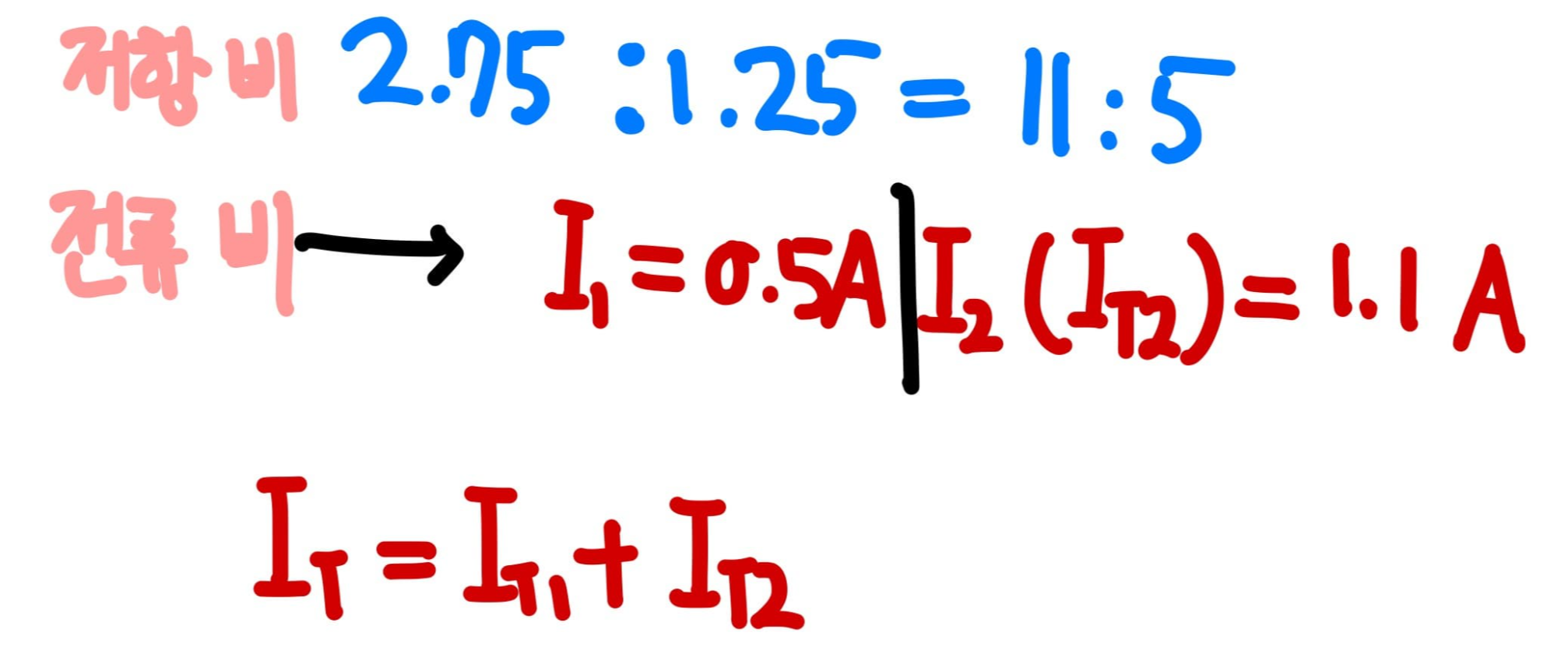
전압이 같을 때 전류와 저항은 반비례하는 성질을 이용합니다.
회로에서 2Ω과 연결되는 두 병렬 저항의 비는 11:5입니다.
두 저항의 전압강하가 같으려면 전류의 비는 11:5가 되어야 합니다.
1.25Ω 저항에 흐르는 전류는 1.5A입니다.
정답 및 마무리
두 회로에서 구한 전류($I_{T}$)를 합치면 됩니다.
1.1A +1.5A =2.6A
회로 시뮬레이션에서 $I_{T}$ 값이 2.6이라는 것을 확인할 수 있습니다.
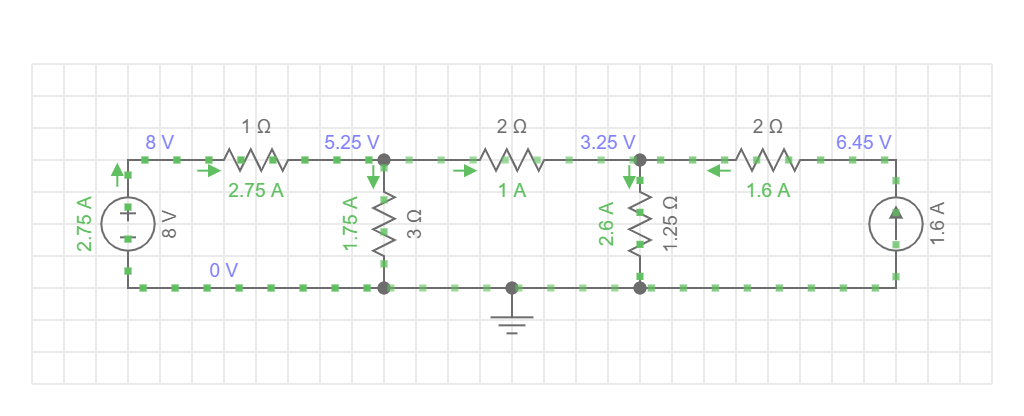
마무리
- 회로의 전원 개수(2개)만큼, 회로를 쪼갭니다.
- 회로 1에서 먼저 전압과 전류의 값을 구합니다.
- 회로 2에서 전압과 전류의 값을 각각 구합니다.
- 쪼갰던 전류, 전압값을 중첩시켜 답을 구합니다.
중첩의 정리에서는 간소화를 유의해야 합니다.
노드, 메쉬해석법은 회로를 변형시키지 않습니다.
등가회로로 바꾸는 방식은 회로를 변형시킵니다.
밖에서 볼 때 원형과 같은 것이지, 내부가 같은 것이 아닙니다.
만일 테브난을 적용한다면, 답을 구할 전류는 바꾸면 안 됩니다.
이 부분에 유의해서 중첩의 정리를 적용해 봅시다.
'회로이론 > 처음해보는 회로이론' 카테고리의 다른 글
| 기초 회로 이론 20. 종속 전원(종속전압원, 종속전류원) (0) | 2023.04.24 |
|---|---|
| 기초 회로 이론 18. 테브난의 정리vs노튼의 정리 비교(전원 변환) (0) | 2023.04.21 |
| 기초 회로 이론 17. 노튼의 정리(노튼 등가회로) 및 예제 (0) | 2023.04.21 |
| 기초 회로 이론 16. 테브난 정리(테브난 등가회로) 및 예제 (3) | 2023.04.18 |
| 기초 회로 이론 15. 폐회로, 개회로(구분방법, 단락 상태, 개방 상태) (0) | 2023.04.15 |




댓글